Построение Контрольных Карт Шухарта
10.2 Типы контрольных карт Шухарта. Типы ККШ различаются по тому, измеряем ли мы какой-либо. Читать тему online: Примеры построения контрольных карт Шухарта с использованием ГОСТ Р 50779.42. Рассматривается использование контрольных карт Шухарта как одного из инструментов.
Содержание. Цели и задачи Цель построения контрольной карты Шухарта — выявление точек выхода процесса из стабильного состояния для последующего установления причин появившегося отклонения и их устранения.
Задачи построения контрольной карты Шухарта:. определить границы системной вариативности процесса,.
спрогнозировать поведение процесса в ближайшем будущем на основе прошлых данных о процессе. Выходящий параметр процесса всегда имеет изменчивость вследствие воздействия различных факторов (кратковременных отклонений входов и внутренних параметров). Таких факторов обычно много, и поэтому они частично компенсируют друг друга. Вследствие этого в стабильном состоянии выходы процесса лежат в определённом коридоре — зоне системной вариабельности процесса. Вероятность выхода параметра за пределы этого коридора не равна нулю, но, как правило, мала. При введении контрольных карт в организации важно определить первоочередные проблемы и использовать карты там, где они наиболее необходимы.
Сигналы о проблемах могут исходить от систем управления дефектами, от претензий потребителей, от любых процессов организации. Элементы графика Контрольные границы — коридор, внутри которого лежат значения при стабильном состоянии процесса. Контрольные границы рассчитываются по формулам, жестко привязанным к типу карты. Эти границы вычисляются по данным о процессе, и никак не связаны с допусками.
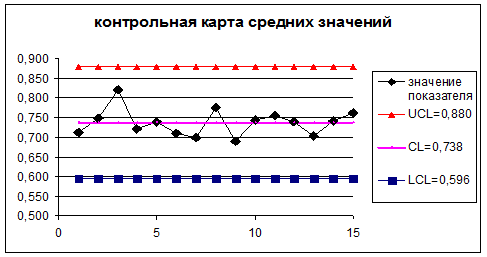
CL — центральная линия (обычно среднее значение или медиана по некоторому объёму данных). LCL — нижняя контрольная граница (нижняя граница спецификации). UCL — верхняя контрольная граница (верхняя граница спецификации) Признаки особой изменчивости процесса Признаки особой изменчивости сигнализируют о нарушении стабильности (управляемости) процесса:. выход точек за верхнюю или нижнюю границы контрольной карты.
7 или более точек подряд лежат по одну сторону от средней линии. более 6 точек монотонно возрастают или убывают Есть и другие признаки (см. Книгу Уилера, Чамберса). Установившегося общепринятого набора дополнительных правил чтения контрольных карт нет, поэтому рекомендуется использовать в первую очередь правило Шухарта (выход точек за границы), а все прочие вводить по мере накопления опыта при необходимости. Виды контрольных карт по шкале измерения карты бывают. качественные.
количественные По выборочному параметру карты бывают. индивидуальных значений. скользящих размахов. среднего.
среднеквадратического отклонения. медианы. размаха и многие другие.
Также. Литература. Уилер Дональд, Чамберс Дэвид. Статистическое управление процессами: Оптимизация бизнеса с использованием контрольных карт Шухарта = Understanding Statistical Process Control. — М.:, 2009. — С. 310. —. Система Шухарта — Н.Новгород: ООО СМЦ «Приоритет», 2004. — 65 с. —.
Барабанова О.А. Семь инструментов контроля качества. — М.:, 2001. — С. 88. Advanced Topics in Statistical Process Control: The Power of Shewhart's Charts. — SPC Press, 1995.
На Викискладе Ссылки.
В настоящей заметке представлены удобные шаблоны в Excel для построения контрольных карт Шухарта. Если эта тема для вас новая, предлагаю начать с книги Д. Существует много видов контрольных карт (см., например,. Статистические методы. Контрольные карты Шухарта). Но основных – два: карта средних и индивидуальных значений. Если контролируемый процесс устроен так, что некоторые значения образуют естественные группы, то рекомендуется использовать контрольную карту средних.
Исходные данные следует собрать в группы, рассчитав для каждой из них среднее значение и размах (размах – разность между максимальным и минимальным значением в группе; рис. Исходные данные для построения карты среднего и размаха Скачать заметку в формате или, примеры в формате Рекомендуется накопить 20–30 средних значений, и уже по ним строить карту. Карта среднего и размаха содержит два графика (рис. 2), на верхнем – карта среднего, на нижнем – карта размаха. На карте среднего отображают средние значения отдельных групп, а также три линии: центральную (среднее средних) и две контрольные границы – верхнюю и нижнюю. Если расчетное значение для нижней границы меньше нуля, эту границу, либо не наносят на карту, либо проводят на отметке ноль. На карте размаха, присутствуют аналогичные данные.
Нижняя контрольная граница, как правило отсутствует. Границы рассчитывают по следующим формулам: UCL X̅ = X̿ + A 2R̅ – верхняя граница карты средних; CL X̅ = X̿ – центральная линия карты средних; LCL X ̅ = X̿ – A 2R̅ – нижняя граница карты средних; UCL R = D 4R̅ – верхняя граница карты размахов; CL R = R̅ – центральная линия карты размахов; LCL R = D 3R̅ – нижняя граница карты размахов.
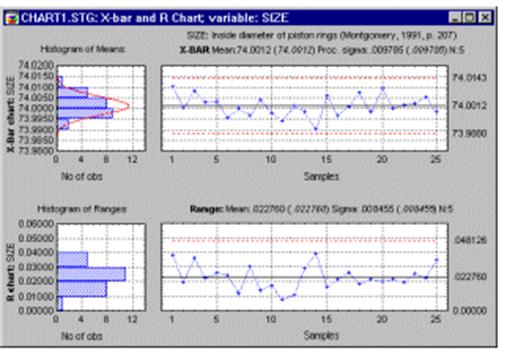
Здесь Х̅ – среднее значение в одной выборке, X̿ – среднее по нескольким значениям средних Х̅, R̅ – среднее по размахам в нескольких выборках, A 2, D 3, D 4 – коэффициенты, зависящие от размера выборок n (рис. При построении карты на рис. 2 использованы 30 первых значений. Карта среднего и размаха; значение D 3 для n = 4 отсутствует, поэтому нижней границы на карте размаха нет Рис. Константы для контрольных карт среднего и размаха (A 2, D 3, D 4) и индивидуальных значений (d 2) Если данные образуют некий ряд, не подлежащий группировке, применяются карты индивидуальных значений и скользящего размаха.
Они получили название XmR-карт. Скользящий размах есть модуль разности последовательных значений (рис. 4; использованы данные из столбца В на рис. Исходные данные для построения XmR-карты Для XmR-карты границы рассчитывают по следующим формулам: нижняя граница карты размахов отсутствует. Здесь – средний скользящий размах, а значения коэффициентов d 2 и D 4 берутся для n = 2 (см рис. Потому что карта скользящего размаха фактически использует группы из двух последовательных измерений для вычисления размаха. Для расчета всех линий использованы первые 30 значений. Гост р 55201 2012 бланк.
XmR-карта индивидуальных значений и скользящего размаха Если сравнить карту средних (рис. 2) и индивидуальных значений (рис.
5), видно, что последняя обладает большей волатильностью, и диапазон между нижней и верхней контрольными границами шире. Это не удивительно, так как на карте средних используется усреднение по четырем значениям. Если выполнить усреднение по еще большему числу значений, границы станут еще ближе.
Важным моментом при построении контрольных карт является использование двух статистик: средних и размахов. Часто используемый неверный способ расчета контрольных границ заключается в том, что используется лишь одна статистика. Например, при построении карты как на рис. 5, использовались бы только индивидуальные значения и их дисперсия. В этом случаев границы рассчитывались бы по следующим формулам: Поскольку при таком подходе используется единая статистика рассеяния, карты размахов в данном случае нет.
Вычисление контрольных пределов, основанное на использовании единой статистики рассеяния, приведет к неправильному результату. Подобные вычисления приводят к расширению полосы между контрольными пределами. Правильный путь вычисления контрольных пределов для карты индивидуальных значений всегда должен использовать двухточечные скользящие размахи. Эта заметка была полностью переработана в октябре 2016 г. Оказалось, что в первоначальном варианте я предлагал неверное решение. С первоначальным вариантом, представляющим лишь исторический интерес, можно ознакомиться. Возможно вас также заинтересует.
Андрей, возможно, я чего-то не понял в Вашем замечании но среднеквадратичное отклонение и стандартное отклонение (сигма) это синонимы. См., например, Википедию. Чамберс «Статистическое управление процессами» довольно много разнообразных правил построения контрольных карт. Я использую одно из них. В какой-то мере, я согласен, что мои построения не слишком строгие, и, возможно, не соответствуют приведенному Вами ГОСТу, но Шухарт вкладывал именно экономический смысл в определение границ. В этом я ему не противоречу 🙂.
Построение Контрольных Карт Шухарта Пример
Алексей, я читал указанную замечательную статью Юрия Павловича Адлера. В этом месте готов поспорить Работы Шухарта на русский язык не переводились, а моего английского недостаточно, чтобы читать в оригинале. Но, как я понял Деминга (см., например, Выход из кризиса, глава 11), границы контрольной карты напрямую зависят от среднего размаха изучаемой выборки, т.е., являются не константами, а зависят от анализируемых данных. У Демнга в качестве оценки кучности данных используется размах, но стандартное отклонение однозначно связано с размахом коэффициентами. Поэтому я и считаю, что верхняя и нижняя границы контрольной карты есть функция средней величины и стандартного отклонения (чтобы увеличить рисунок кликните на нем правой кнопкой мыши и выберите «Открыть картинку в новой вкладке»). Здравствуйте, Сергей.
Я менеджер по качеству одной частной маленькой компании по производству пластиковых авто компонентов. Я недавно ушёл с одной западной известной автомобильной компании (со сборочного производства) и устроился на новую работу. Естественно в маленькой российской компании технологи и производственники понятия не имеют о таких инструментах качества, как SPC и MSA (только в общих чертах). Поэтому мне пришлось включать опыт и мозги, чтобы с нулевым бюджетом как-то внедрить эти инструменты.
Построение Контрольных Карт Шухарта
Спасибо Вам за ваш сайт, в частности данный блог. Благодаря последнему смог внедрить в производство control chart, не покупая сторонние программы. На Вашу личную почту я скинул пару шаблонов с Xbar-R и I-MR картами, и вместе с этим хотел только попросить Вас, чтобы Вы, так сказать, проверили мои файлы и формулы в них (взгляд со стороны), а также можете эти файлы опубликовать у себя на сайте (я не против), чтобы другие не мыкались и могли сразу использовать готовые шаблоны.